Jak vypočítat procenta

Počítání procent není složitá ani zdlouhavá záležitost, pokud víte jak na to a znáte základní princip. Jak vypočítat procenta podle několika různých metod se dozvíte v následujících odstavcích. Zároveň většina z nás využívá procenta v běžném životě, ať už počítáme daně, řešíme úroky nebo bychom rádi zjistili, jakou slevu nabízí prodejce. Po přečtení tohoto článku už vás žádné procentuální hodnoty nepřekvapí.

Procenta – základní vysvětlení

Pro správný výpočet procent je třeba znát základní pojmy.

• Základ – jedná se o celek se kterým chceme manipulovat
• Procentová část – procenta přepočítaná na absolutní hodnotu
• Počet procent (%) – vyjádření relativní části celku

Základ tvoří 100 %. Jedno procento tedy tvoří setinu z celku. Např.: 35 % můžeme vyjádřit i jako zlomek: 35/100.

Výpočet procentové části

Nejdříve si definujeme, co je to procentová část. Jedná se o část základu, kterou můžeme vyjádřit procenty. Výpočet procentové části využijeme v případě, kdy známe základ a známe počet procent a chceme vypočítat, kolik je daný počet procent v absolutních hodnotách.

Nejlépe si vysvětlíme celý proces na příkladu:

Zaměstnavatel nám uvede hrubou mzdu 20 000 Kč, to je základ. Daň z příjmu fyzických osob je 15 %, pokud chceme zjistit, kolem zaplatíme státu na daních, postup je následovný:

• Základ – 20 000 = 100 %
• Počet procent – 15 %
• 1% ……… 20 000 % 100 = 200

Hodnotu jednoho procenta vynásobíme patnácti a zjistíme, kolik zaplatíme státu na daních, to je naše procentová část.

200 x 15 = 3000

Procentová část je tedy 3000 Kč.

Obecně, ať už máme jakoukoli procentovou část, vždy je snadné jít přes hodnotu jednoho procenta. V tomto postupu neuděláte chybu.

Výpočet procent z celku

Za celek považujeme základ, se kterým dále počítáme. Tento typ výpočtu použijeme například při výpočtu daní, kdy známe hrubou mzdu a procentuální hodnotu daně. Jako základ si vezmeme například 500, což je 100 %. Pokud chceme zjistit, kolik je 20 % z celku, postup je následovný:

• 500 = 100%
• Nejdříve získáme hodnotu 1 %
• 500 : 100 = 5
• 1 % = 5
• Z tohoto údaje získáme hodnotu 20 %
• 5 x 20 = 100
• Z toho vyplývá, že 20 % z celku je přesně hodnota 100.

Použití trojčlenky při počítání procent

Procenta lze počítat i za využití trojčlenky, kterou všichni důvěrně známe už z dob základní školy. Postup je obdobný jako u klasické trojčlenky, jenom si musíme uvědomit, co, a hlavně kam dosadíme. V případě procent se vždy jedná o přímou úměru.

Uvedeme si to na příkladu:

Základ máme 8000 a chceme zjistit, kolik je 60 % z tohoto základu:

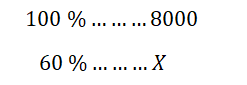
Z tohoto základního předpisu trojčlenky vytvoříme díky přímé úměře jednoduchou rovnici:

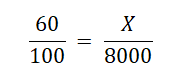
Dále řešíme rovnici o jedné neznáme, v tomto případě vynásobíme rovnici 8000 a získáme:

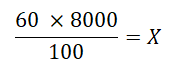
Vyřešíme zlomek a dostaneme výsledek:

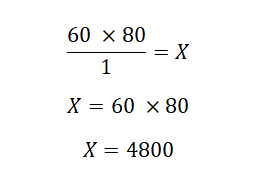
Z výsledku tedy můžeme říct, že 60 % ze základu 8000 je přesně 4800.

Trojčlenku můžeme použít i v případě, že neznáme hodnotu základu, ale víme procentovou část a počet procent.

Například víme, že ve třídě je momentálně 18 žáků, což je 60 % z celé třídy. Chceme zjistit, kolik žáků je ve třídě celkově.

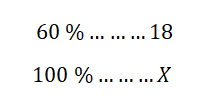
Z tohoto vytvoříme zlomek:

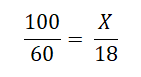
A dále postupujeme jako v předchozím příkladu:

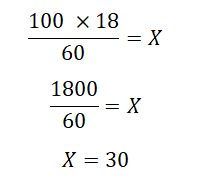
Z výpočtu víme, že celkový počet žáku ve třídě je 30.

Výpočet procent z ceny zboží

Výpočet procent z ceny využíváme zcela běžně například při nákupu v obchodě nebo na internetu, případně při výpočtu DPH.

Obecně při výpočtu procent z ceny používáme dva postupy.

Známe plnou cenu a chceme odečíst procentuální část (např.: DPH nebo slevu, kterou nabízí prodejce)

Jako základ, tedy 100 % máme plnou cenu zboží, například 1500 kč, procentuální část (sleva) je 40 %. Na začátku si musíme uvědomit, že cena po slevě tedy bude 60 % původní ceny

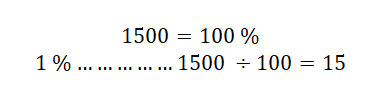
1 % z 1500 kč je tedy 15 kč

Teď můžeme postupovat dvěma způsoby. Buď vynásobíme 15 kč hodnotou 40 %, získáme hodnotu slevy a tu odečteme od původní ceny nebo vynásobíme 15 kč hodnotou 60 % a získáme cenu po slevě.

15 x 40 = 600 ….. hodnota slevy je 600 kč

1500 – 600 = 900 ….. cena po slevě je 900 Kč

 15 x 60 = 900….. Přímé vypočítání ceny po slevě

Známe cenu po slevě a procentuální hodnotu slevy

V tomto případě chceme zjistit základ, tedy cenu produktu před slevou. Pracujeme s cenou po slevě a v procentuální hodnotou slevy.

Cena po slevě – 1700 kč

Sleva – 15 %

Nejdříve si přepočteme, že cena po slevě, je vlastně 85 % původní ceny (100 % – 15 % = 85 %)

1700 = 85 %

Z toho zjistíme, kolik je hodnota 1 %

1700 / 85 = 20

Hodnota 1 % je tedy 20 kč.

Teď už stačí pouze vynásobit tuto hodnotu stem a získáme 100 % a tedy hodnotu celku a původní cenu.

20 x 100 = 2000

Původní hodnota produktu je 2000 kč.

Příklady použití procent

Jak se počítají procenta v praxi si ukážeme na několika příkladech z běžného života.

Daňové účetnictví

Při počítání hodnoty 15 % daně z příjmu využijeme počítání procent, např. máme-li hrubou mzdu 23 500 Kč, postup bude následovný:

23 500 / 100 = 235
235 x 15 = 3525

Státu odvedeme na daních 3525 Kč.

Slevy zboží

Tradičně se nás prodejce snaží nalákat na velké slevy, abychom zjistily, jaká je vlastně hodnota slevy, použijeme následující postup. U většiny zboží máme uvedenou cenu po slevě a procentuální hodnotu slevy. Pokud chceme vědět, kolik věc původně stála, musíme se dopočítat základu, např. cena po slevě je 1275 Kč a sleva byla 15 %. Kolik byla původní cena zboží?

1275 / 85 = 15
15 x 100 = 1500

Původní cena zboží byla 1500 kč.

Úroky při půjčce

Půjčujete si peníze a každá banka nebo nebankovní ústav vám určí úrokovou sazbu, tedy procentuální vyjádření toho, co splatíte navíc, kromě půjčené částky, např. chcete si půjčit 150 000 kč a úroková sazba je 8 %. Kolik finálně zaplatíte včetně půjčené částky?

150 000 / 100 = 1500
(100 + 8) x 1500 = 162 000

V závorce sčítáme 100 % – tedy částku kterou si půjčujeme a 8 % – tedy úroky, které musíme zaplatit.

Bance splatíte včetně úroků 162 000 kč.

Storno poplatky

Velice často si cestovní kanceláře nebo hotely určují tzv. storno poplatky, tedy procento z ceny, které musíte zaplatit, pokud pobyt zrušíte. Pokud je cena zájezdu např. 7500 kč a storno poplatek je 70 %, kolik zaplatíte v případě, že zájezd zrušíte?

7500 / 100 = 75
75 x 70 = 5250

Storno poplatek tedy činí 5250 kč.

Daň z přidané hodnoty

V České republice je základní sazba DPH 21 %. Pokud kupujeme zboží jako běžný kupující, 21 % z ceny každé položky odchází státu jako daň z přidané hodnoty. V určitých případech se můžeme placení DPH vyhnout (některé subjekty nejsou plátci DPH). Zjištění hodnoty daně si uvedeme na jednoduchém příkladu. Zmrzlina stojí v obchodě 119 kč, kolik korun je DPH?

119 / 121 * 21 = 20,652

Státu tedy v rámci DPH zaplatíme 20,65 Kč z ceny zmrzliny.

Procenta – slovní úlohy

V následujících odstavcích si ukážeme, jak z textu udělat snadný příklad a vypočítat jej.

• V menu v restauraci je v nabídce 6 salátů, 5 hotových jídel a 9 rychlovek. Kolik procent z jídelníčku tvoří jednotlivé kategorie?

Nejdříve si vytvoříme základ, tedy 100 %: 6 + 5 + 9 = 20

Dále už jen získáváme jednotlivá procenta

Hotová jídla
5 / 20 = 0,25
0,25 x 100 = 25%

Saláty
6 / 20 = 0,3
0,3 x 100 = 30%

Rychlovky
9 / 20 = 0,45
0,45 x 100 = 45%

• V obchodě jsme koupili láhev, která obsahuje 37% alkoholu. Obsah lahve je 0,7 litru. Kolik mililitrů alkoholu najdeme v lahvi?

Základ – 0,7 litru = 700 ml = 100%
1% ……. 700 / 100 = 7
7 x 37 = 259

Láhev obsahuje 259 ml čistého alkoholu.

• Při nakupování si nastavíte limit 2000 kč, u pokladny zjistíte, že máte nákup za 1850 kč. Kolik procent z limitu jste utratili?

2000 = 100 %
1850 / 2000 = 0,925
0,925 x 100 = 92,5 %

Utratili jste 92,5 % ze svého limitu

• Při jiném nákupu jste si nastavili limit 1500 kč, ale u pokladny jste zjistili, že jste překročili limit a nákup stál 1780 kč. O kolik jste překročili limit?

1500 = 100%
1780 / 1500 = 1,1867
1,1867 x 100 = 118,67 %

Limit jste překročili o 18,67 %.

• Ve škole je dohromady 680 žáků. Většina jsou praváci, ale 10 % jsou leváci. Kolik leváků je ve škole?

680 / 100 = 6,8
6,8 x 10 = 68

Ve škole je 68 žáků leváků.

Tip: v těchto příkladech, kdy řešíme podíl 10 % většinou stačí posunout desetinnou čárku.

Výpočet procent v MS Excel

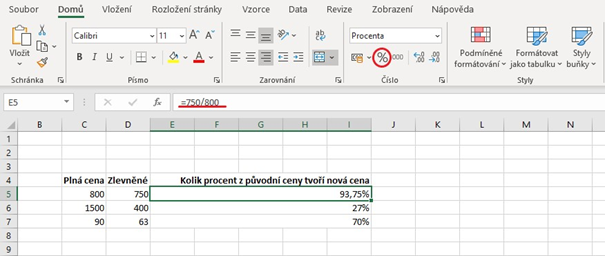
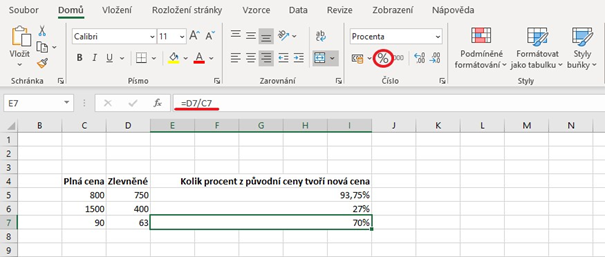
Výpočet procent v Excelu je snadný. Buď můžeme zadat vzorec přímo do buňky (obrázek 1) nebo můžeme počítat z různých buněk (obrázek 2). Pokud chceme, aby se nám v buňce zobrazil pouze výsledek, musíme začít znakem „=“ a pak teprve zadat data nebo buňky. Nesmíme zapomenout, že počítáme s procenty, tedy danou buňku musíme převést do režimu „Procenta“ (červený kroužek), výsledná hodnota se převede z desetinných čísel do procent.

Obr. 1

Obr. 2

Jak počítat procenta na kalkulačce

Procenta na kalkulačce počítáme stejně jako na papíře nebo z hlavy. Musíme si ujasnit postup a pak jej následovat. Nejjednodušší je zadávat jednotlivé kroky postupně a mezivýpočty si zapamatovat nebo zapsat na papír. Pokud bychom chtěli zadat celý výpočet najednou bude zapotřebí použití závorek pro upřesnění pořadí a na to bychom potřebovali matematickou kalkulačku.

Tradičně požívané symboly na běžné kalkulačce

+ _ sčítání

– _ odčítání

* nebo × _ násobení

÷ _ dělení

Postup u příkladu by byl tedy následovný.

Základ máme 7500 a chceme zjistit kolik je 15 %.

Na kalkulačce zadáme:  7500 ÷ 100 a výsledek vynásobíme patnácti a dostaneme konečný výsledek, tedy hodnotu patnácti procent.